El término Efecto Mariposa fue introducido en el año de 1972 por Edward Norton Lorenz, brillante matemático y meteorólogo que estableció las bases de la predictibilidad del clima y a quien se le considera como el fundador de la teoría moderna del caos.
Este término fue introducido por Lorenz en el título de su artículo: ¿El aleteo de una mariposa en Brasil puede provocar un tornado en Texas?
Y no es que esto realmente pase, si no que sirve a manera de ejemplificar de que un cambio pequeño en las condiciones iniciales de un sistema puede tener un cambio significativo en sus estados posteriores.
Lorenz laboraba en el departamento de pronóstico del clima cuando un día, trabajando con ciertos valores, encontró algo desconcertante. Realizó cálculos con valores a 6 decimales y después repitió los mismos pero con los valores redondeados a 3 decimales. La primera y segunda gráfica inicialmente eran prácticamente iguales pero después de un tiempo ambas eras completamente diferentes.
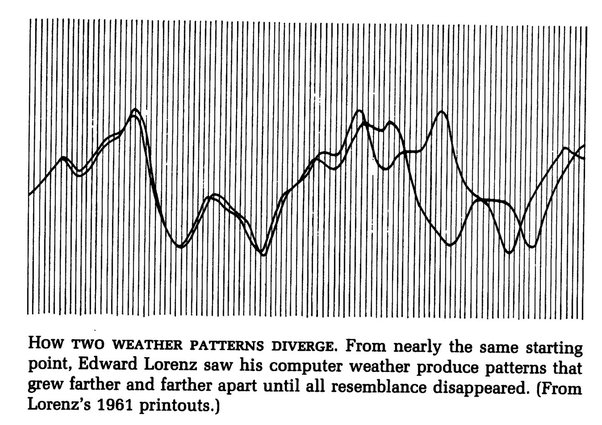
Una diferencia de 0.001 produjo grandes cambios en el sistema. Fue en ese día cuando Lorenz dió inicio a la teoría del caos.
¿Pero, qué es un sistema caótico?
Un sistema caótico es un sistema dinámico sensible a condiciones iniciales. El péndulo doble es un sistema que ejemplifica de buena manera este comportamiento caótico.
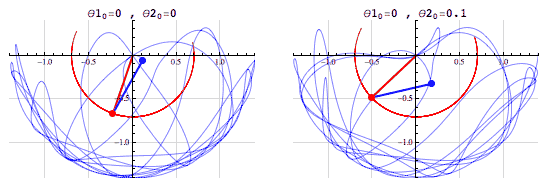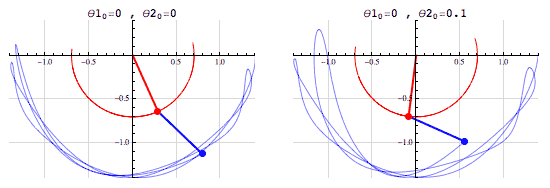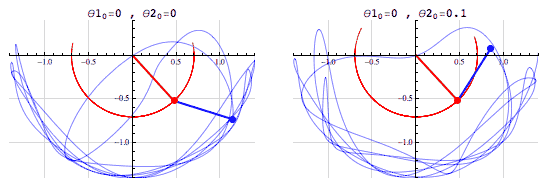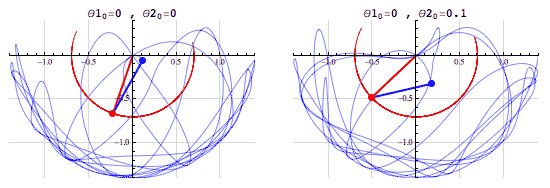
En el primer sistema θ20 = 0 y en el segundo θ20 = 0.1. Esta pequeña diferencia en θ20 ha llevado a que los dos sistemas evolucionen de una manera muy diferente en el tiempo.
Es interesante el hecho de que aunque conocemos las ecuaciones que gobiernan la dinámica de un péndulo doble, surja la duda sobre si este sistema es impredecible o determinista.
Los sistemas caóticos son deterministas dado que conocemos las ecuaciones que los gobiernan y, si hiciéramos una simulación en computadora con un conjunto de condiciones iniciales conoceríamos la evolución del sistema a través del tiempo, pero en la práctica al tratar de replicar el sistema tendríamos resultados completamente diferentes a la simulación que hicimos en computadora ya que no podríamos ajustar con exactitud de infinitos decimales las condiciones iniciales, generando un sistema completamente diferente. Este aspecto agrega la impredecibilidad a los sistemas caóticos.
Lorenz obtuvo 3 ecuaciones con 3 variables para sus cálculos sobre la predicción del clima:

Este sistema aunque es caótico ejemplifica la utilidad de estos sistemas: aunque sea imposible predecir el comportamiento para cada condición inicial individual, si es posible ver como se comportan todas en conjunto. El sistema de ecuaciones (1) forma esta figura en el espacio fase:

Cada condición inicial sigue una trayectoria única que nunca se cruzará con ella misma ni con la trayectoria para otra condición inicial diferente. Esta figura se conoce como atractor de Lorenz e increíblemente tiene la forma de una mariposa.
