¿Cuál es la conexión entre una población ya sea de conejos, personas o algún otra especie, la convección térmica en un fluido y la activación de neuronas en tu cerebro?.
Comenzaremos hablando de una aplicación logística en la población la cual es una relación de recurrencia, este modelo es a menudo citado como un ejemplo de representación de lo complejo que puede ser un comportamiento caótico aunque se parta de un modelo de sencilla expresión. Dicho modelo puede ser simplemente el siguiente:
(1) 
Donde 
es la poblacion al año siguiente, 
es la población actual y r es la tasa de crecimiento de esta poblacion, pero este modelo presenta un pequeño problema el cual es que a una población inicial con una tasa de crecimiento cualquiera implica que su aumento seria exponencial para siempre, por lo que es necesario agregar restricciones del entorno, siendo ahora:
(2) 
Ahora es un modelo sencillo que tiene restricciones y nos representa una buena aplicación logística, aunque este modelo parezca sencillo puede tender al caos, por ejemplo a valores diferentes de la tasa de crecimiento esta población tiende una estabilización sin importar su población inicial dependiendo solo de su tasa de crecimiento r al iterarlo como se muestra a continuación.
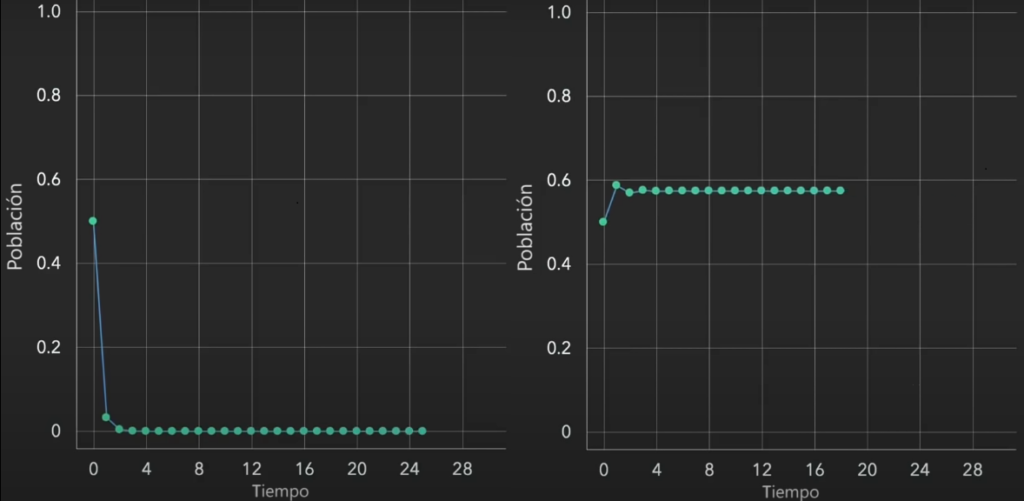
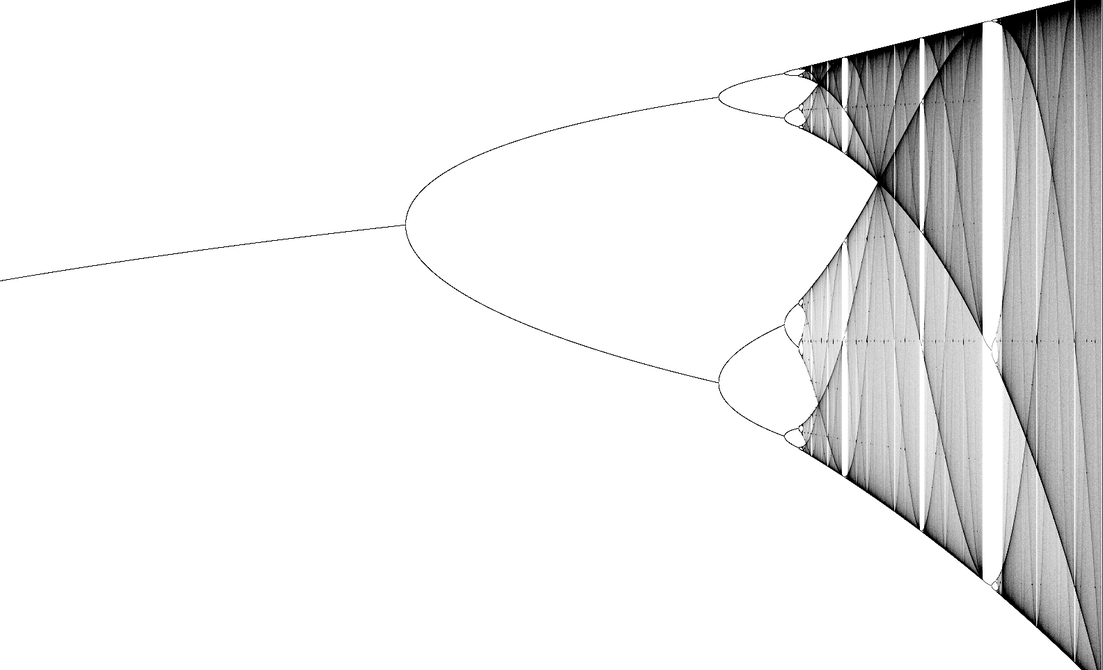
En a) la población tiende a extinguirse mientras que en b) a la estabilidad, pero que pasa cuando la tasa de crecimiento supera el valor de 3, ocurre una bifurcación repitiéndose en forma periódica en ciclos diferentes ocasionando el caos y ciertos periodos de estabilidad.
Esta ecuación parece modelar entonces poblaciones de animales, pero hace falta relacionarlo con otras áreas de la ciencia sin relación entre si. La primera confirmación importante de esta aplicación logística vino de Lib Taber, su investigación sobre un fluido con un gradiente de temperatura dentro de dos tubos con rotación inversa resulto en la confirmación de este modelo en un experimento, lo mismo ocurrió con la respuesta de los ojos ante las luces parpadeantes; cuando la luz alcanza cierto índice de parpadeo los ojos solo responden a ciertos parpadeos resultando en este mismo modelo logístico antes mencionado para la población de animales.
Estos estudios influido en la medicina, se uso el caos para controlar un corazón y descubrir una manera mas inteligente de administrar cargas eléctricas para que volviera a latir normalmente. Esta diagrama parece aparece en tantos lugares que el físico Mitchell Feigenbaum analizo cuando aparecen las bifurcaciones y encontró que la relación se acerco a 4.669, pero no parece estar relacionada con ninguna otra constante física conocida por lo que es en si misma una constante fundamental de la naturaleza. Dichos diagramas no solo ocurren con la ecuación planteada al inicio, sino también en toda aquella función de parábola iterada con la misma relación de las bifurcaciones, es decir, toda aquella función que sea como:
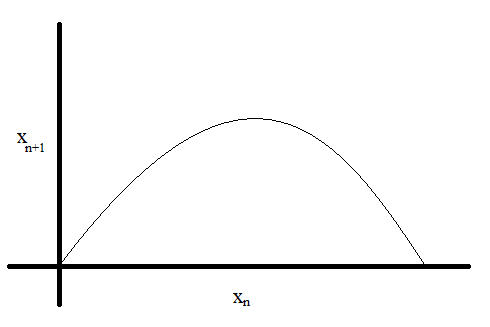
Por lo que se puede apreciar que a pesar de ser una ecuación tan sencilla puede ocasionar el caos y aparecer en lugares que uno no a imaginado.