¿Qué es un Autómata Celular? - PhD Alejandro Puga

Son sistemas descubiertos dentro del campo de la física computacional en los 40s pon John Von Neumann y posteriormente por John Horton Conway y Stephen Wolfram, John Von Neumann intentaba modelar una maquina capaz de auto-replicarse, formalmente definido como un modelo matemático computacional para un sistema dinámico que evoluciona en pasos discretos compuesto por un conjunto de celdas o células que adquieren distintos estados o valores los cuales son alterados de un instante a otro, es decir, en pasos discretos los cuales pueden cuantificarse con valores enteros a intervalos regulares e interpretados como una maquina con reglas complicadas sobre una red rectangular. Su nombre se debe a la similitud con el crecimiento de las células. De esta manera este conjunto logran una evolución según una determinada expresión matemática, que evoluciona de acuerdo a los estados de las células vecinas, conocida como regla de transición local. su rasgo característico es que son una tupla, es decir, su capacidad de lograr una serie de propiedades que surgen de la propia dinámica local a través del paso del tiempo y no desde un inicio, aplicándose a todo el sistema en general , complejo por naturaleza, por medio de una simulación, partiendo de un estado o configuración inicial de células y cambiando en cada instante los estados de todas ellas de forma síncrona.

Elementos Básicos de un Autómata Celular

Espacio regular. Ya sea una línea, un plano de 2 dimensiones o un espacio n-dimensional. Cada división homogénea del espacio es llamada célula.

Conjunto de Estados. Es finito y cada elemento o célula del espacio puede tomar un valor en ${ \mathbb {Z} }$ a partir de un conjunto finito de estados $k$ . También se denomina alfabeto. Puede ser expresado en valores o colores.

Configuración Inicial. Es la asignación inicial de un estado a cada una de las células del espacio.
Vecindades. conjunto de células finito que se consideran adyacentes a una célula dada, así como la posición relativa respecto a ella. Cuando el espacio es uniforme, la vecindad de cada célula es isomorfa.

Función de Transición Local. Es la regla de evolución que determina el comportamiento del AC a partir del estado de la célula y su vecindad. Define cómo debe cambiar de estado cada célula dependiendo su estado anterior y de los estados anteriores de su vecindad. Suele darse como una expresión algebraica o un grupo de ecuaciones.

Tipos de fronteras

Frontera Abierta. Se considera que fuera del espacio regular donde residen las células, todas con un valor fijo. En el caso particular del juego de la vida y de otros AC con dos estados en su conjunto $k$ , una frontera se dice fría si las células fuera de la frontera se consideran muertas, y caliente si se consideran vivas.
Sin Frontera. La representación autómata no tiene limites, es infinito y por lo tanto se crea un nuevo vecino adicional en la frontera al llegar a ella.
Frontera Reflectora. Las células fuera del espacio del autómata toman los valores que están dentro, como si se tratara de un espejo, es decir, reflejan los valores de aquellas dentro
Frontera Periódica o Circular. las células que están en la frontera interaccionan con sus vecinos inmediatos y con las células que están en el extremo opuesto del espacio, como si lo dobláramos en forma de cilindro.

Clasificación de los Autómatas Celulares

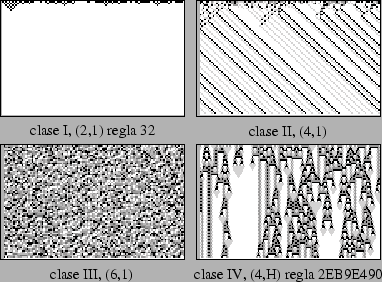
Puede ser clasificados en tres etapas asociadas a los nombres de los científicos que en cada momento marcaron un punto de inflexión en el desarrollo de la teoría: la era de Von Neumann, la era de John Horton Conway y la era de Stephen Wolfram. Von Neumann implementa la teoría de los autómatas celulares en un vector de dos dimensiones, John Horton Conway dio a conocer el autómata celular que probablemente sea el más conocido: el Juego de la vida. Pero mas importante Stephen Wolfram trabajo en autómatas celulares a mediados de 1981, realizado numerosas investigaciones sobre el comportamiento cualitativo de los A.C. y descubrió patrones complejos que parecían formarse. Sus investigaciones fueron inicialmente impulsados por un interés en sistemas de modelado, como las redes neuronales. En 2002 Wolfram publicó un texto de 1.280 páginas, A New Kind of Science, que sostiene ampliamente que los descubrimientos sobre autómatas celulares no son hechos aislados sino que son robustos y tienen importancia para todas las disciplinas de la ciencia. Con base en su trabajo sobre AC unidimensionales, con dos o tres estados, sobre configuraciones periódicas que se presentan en el AC, observó sus evoluciones para configuraciones iniciales aleatorias. Así, dada una regla, el AC exhibe diferentes comportamientos para diferentes condiciones iniciales, la clasificación de Wolfram fue el primer intento de clasificación global del comportamiento cualitativo de los AC unidimensionales. En orden de complejidad las clases son:

Clase I: La evolución lleva a una configuración estable y homogénea, es decir, todas las células terminan por llegar al mismo valor.
Clase II: la mayoría de los patrones iniciales evolucionan rápidamente hacia estructuras estables u oscilantes (periódicas). Parte de la aleatoriedad del patrón inicial puede permanecer. Los cambios locales en el patrón inicial tienden a permanecer locales.
Clase III: los patrones iniciales evolucionan de forma pseudo-aleatoria o caótica. Las estructuras estables que aparecen son destruidas rápidamente por el ruido circundante.
Clase IV: Casi todos los patrones iniciales evolucionan en las estructuras que interactúan de manera compleja, las estructuras locales pueden ser capaces de sobrevivir por largos períodos de tiempo, es decir, que apareciesen estructuras estables u oscilantes, pero el número de pasos necesarios para llegar a este estado puede ser muy grande, incluso cuando el patrón inicial es relativamente simple, por lo que esta clase es ni completamente caótico, ni completamente ordenado, sino en la línea entre uno y otro, este suele ser el tipo de comportamiento más interesante que un sistema dinámico puede presentar.

http://delta.cs.cinvestav.mx/~mcintosh/comun/tesismaestria/genaro/img149.gif

La importancia de los Autómatas Celulares

Los autómatas celulares se sitúan en el campo de los sistemas complejos, lo que hace muy difícil su definición. Es por ello que el estudio de los sistemas complejos se encuentra en una etapa muy preliminar. Como añadido, las distintas comunidades que pueden encontrar interesante el campo, o para las que podría ser útil, a menudo no mantienen una comunicación demasiado fluída entre sí, con lo que la información está dispersa.

Los autómatas celulares son interesantes por la creencia de que pueden contribuir, quizás de forma substancial, al desarrollo de un punto de vista del mundo en el que lo que vemos deja de convertirse en algo misterioso para convertirse en algo natural. La razón para esta creencia es el hecho de que los autómatas celulares son capaces de generar comportamientos globales con patrones muy complejos sobre la base de unas reglas de interacción muy simples y locales. Además, los autómatas celulares tienen dos virtudes fundamentales: son bien definibles desde el punto de vista matemático y son fáciles de representar utilizando ordenadores.

El paradigma de modelado de los autómatas celulares supone considerar una representación muy especial del espacio, del tiempo y de los estados del sistema lo que, como veremos, los sitúa en el vértice opuesto al ocupado por los modelos matemáticos continuos.

Una de las aplicaciones que tienen los AC en el campo de las finanzas prediciendo aciertos en la predicción de la dirección de las variaciones en los precios, utilizando solamente como variables explicativas los estados del periodo anterior, los que son sometidos a una función de influencia de las comunas vecinas. también pueden aplicarse en el diseño de la función de contagio o influencia.

Ejemplos de Autómatas Celulares

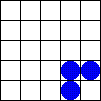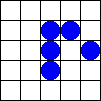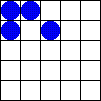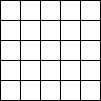
Uno de los AC mas conocidos es el Juego de la Vida creado por John Horton Conway en 1970. El juego consiste en una cuadrícula donde se coloca al inicio un patrón de células «vivas» o «muertas». La vecindad para cada célula son los ocho celdas que la rodean. De manera repetida, se aplican simultáneamente sobre todas las células de la cuadrícula las siguientes 3 reglas:

Muerte: se reemplaza una célula viva por una muerta si dicha célula no tiene más de 1 vecino vivo (muerte por aislamiento) o si tiene más de 3 vecinos vivos (muerte por sobrepoblación). Supervivencia: una célula viva permanecerá en ese estado si tiene 2 o 3 vecinos vivos.
Nacimiento: se reemplaza una célula muerta por una viva si dicha célula tiene exactamente 3 vecinos vivos.

El Juego de la Vida tuvo mucha popularidad gracias a aparición de una nueva generación de computadores económicos en el mercado . Desde su publicación, el juego atrajo mucho interés debido a la gran variabilidad de la evolución de los patrones. icho juego denotaba un ejemplo de auto-replicación y auto-organización similar a los sistemas biológicos. Por esta razón los científicos estudiaron la implementación del juego, observando la forma en la que complejos patrones pueden surgir de la definición de una serie de reglas muy sencillas.

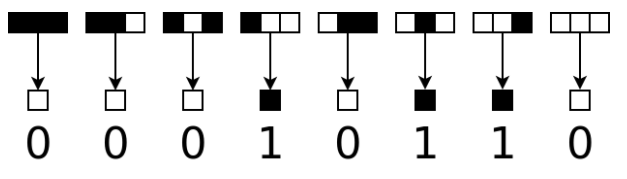
https://www3.gobiernodecanarias.org/medusa/ecoblog/mrodperv/files/2015/12/gameoflife_glider_animation.gif

La regla exactamente 1: Se considera la regla determinada por la tabla

000	001	010	011	100	101	110	111
0	1	1	0	1	0	0	0

Consiste simplemente en poner un 1 si y solo si existe un único 1 en el entorno. El patrón obtenido a partir de la configuración inicial consistente en poner un 1 en posición 0 y ceros en el resto es la siguiente:

Este patrón geométrico corresponde con una figura fractal conocido como el triángulo de Sierpinski. si nos quedamos con uno de los subtriángulos que aparecen dentro de él, obtenemos la misma figura que al inicio: esto se llama autosimilitud y es una característica de los cuerpos fractales. Si ponemos una condición inicial aleatoria el patrón ordenado desaparece y se obtienen formaciones complejas:

La regla de la mayoría La tabla de la regla es la siguiente:

000	001	010	011	100	101	110	111
0	0	0	1	0	1	1	1

Cada autómata calcula cuál es el estado mayoritario en su entorno y se actualiza de acuerdo con la mayoría. En directa la interpretación de los estados 0 y 1 como dos opiniones diferentes en una población o inclinaciones políticas, de modo que el autómata celular queda como:

Ejemplos Bidimensionales

Tendríamos que utilizar tres dimensiones, dos de ellas para el espacio y una más para el tiempo. Si usamos el vecindario de Von Neumann, el vecindario de una célula bidimensional estará formado por nueve células: ella misma y las ocho células que la rodean. Los estados, como en el caso 1d, son dos: 0 y 1.

En este autómata celular, cada célula se actualiza siguiendo el siguiente proceso:

Si la célula está en estado 1 (activada o caliente) entonces permanecerá en estado 1, independientemente de los estados de sus vecinas.
Si la célula está en el estado 0 (inactiva o fría) entonces sumará los estados de las células vecinas. Si el número de celdas activadas en su entorno es 1 o 2, entonces la célula actualizará su estado a 1; en caso contrario permanecerá desactivada.

En las siguientes figuras podemos ver una secuencia en la evolución de esta regla partiendo de la semilla inicial en la que todas las celdas están desactivadas excepto la central. Esta regla se llama de solidificación porque una vez que una célula es activada permacene así para el resto de la evolución.

si la regla es:

Si la célula está en estado 1 entonces permanecerá en estado 1, solo si el número de células vecinas está comprendido entre 0 y 4. En caso contrario se desactivará.
Si la célula está en el estado 0 entonces se activará sólo si número de celdas activas de su entorno es 3 exactamente. En cualquier otro caso permanecerá desactivada.

el resultado es el siguiente partiendo de una pequeña semilla de celdas activadas en el centro.

Autómatas Celulares con más de 2 estados

Si añadimos un posible tercer estado entonces las posibilidades son casi ilimitadas. y la evolución de un autómata celular 1d con tres estados 0,1 y 2, que son representados por tres colores diferentes.

La regla consiste en sumar los estados de las celdas vecinas, obteniéndose un valor comprendido entre 0 y 6. El nuevo estado es asignado en función de la siguiente tabla:

0	1	2	3	4	5	6
1	2	1	1	2	0	2

Con estos ejemplos se puede intuir que los autómatas celulares pueden generan sistemas dinámicos con comportamientos extremadamente diversos con una regla tan simple e incluso desembocando en resultados tan complejos que podrían tener estabilidad en todo ese mar de caos. Es por ello que es interesante utilizarlos en ciencias como modelos de comportamientos complejos ya que pueden predecir ciertos patrones con una configuración inicial en ciertos casos es por ello que en el mundo matemático los autómatas celulares se encuadran como sistemas dinámicos simbólicos.